Principal Component Analysis (PCA)

Principal Component Analysis (PCA) Explained for Laymen

A Simple, Intuitive Guide with Examples

Introduction

In today's data-driven world, we often deal with too much information at once. Whether it's student marks, medical test results, or business data, handling many variables together can become confusing and inefficient.

This is where Principal Component Analysis (PCA) comes in.

PCA is a simple yet powerful technique that helps us reduce complexity without losing important information. In this blog, we'll explain PCA in plain language — no maths, no heavy machine learning jargon.

The Core Problem PCA Solves

Imagine trying to understand something using too many measurements:

• A student evaluated using 10 subjects

• A patient tested using 40 medical parameters

• A business analyzed using 100 performance indicators

More data does not always mean more clarity. Often, many measurements are closely related and repeat the same information.

PCA helps by asking:

"Can we describe this data using fewer, smarter variables?"

What is PCA in Simple Words?

Principal Component Analysis (PCA) is a method that:

• Combines related information

• Finds the most important patterns in data

• Replaces many variables with a few meaningful summaries

Think of PCA as data compression with intelligence.

A Student Marks Example 

Imagine three subjects:

• Maths

• Physics

• English

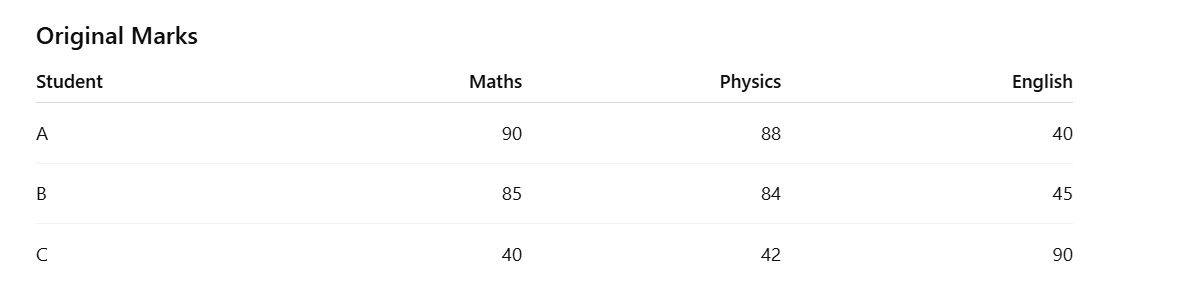
Observations:

• Maths and Physics move together

• English behaves differently

PCA notices this pattern automatically.

What PCA Does Next

Instead of keeping all subjects separately, PCA creates new combined scores:

• PC1: Science Strength (mostly Maths + Physics)

• PC2: Language Strength (English compared to Science)

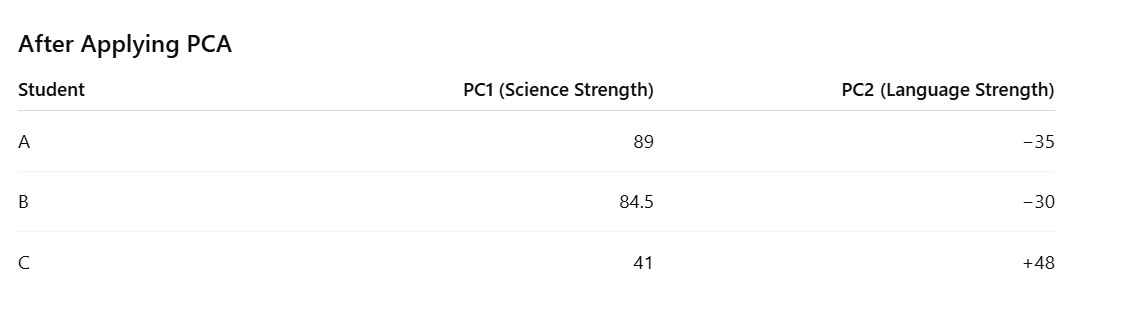
Now:

• 3 subjects → 2 meaningful numbers

• Almost all important information is preserved

• Comparison becomes easier

Why PCA is Called "Unsupervised"

PCA does not know:

• Who passed or failed

• Who is a topper

• Any class labels or outcomes

It only looks at relationships between numbers.

That's why PCA is classified as an unsupervised machine learning technique.

Real-Life Uses of PCA

PCA is widely used across industries:

📸 Image Processing

• Compress images

• Remove noise

• Speed up recognition systems

🏥 Healthcare

• Combine dozens of test results

• Identify overall health indicators

🛒 Business & Marketing

• Understand customer behavior

• Reduce hundreds of features into key traits

🤖 Machine Learning

• Reduce data size before training models

• Improve speed and performance

What PCA Does NOT Do

It's important to understand PCA's limits:

• ❌ It does not predict outcomes

• ❌ It does not classify data

• ❌ It does not understand meaning — only patterns

PCA is about structure discovery, not decision-making.

🩺📄 The "Doctor's Test Report" Cartoon

Panel 1: Too many reports

A doctor is sitting at a desk covered with lab reports:

• Blood sugar

• HbA1c

• Cholesterol

• Triglycerides

• BP

• ECG

• BMI

• Heart rate

The doctor looks overwhelmed 😵 and says:

"So many numbers… what's the big picture of this patient?"

👉 This is high-dimensional data.

Panel 2: PCA enters the clinic

A calm assistant named PCA walks in 🧑‍⚕️✨ and says:

"Don't worry. I'll summarize these tests."

Important:

• PCA does not know if the patient is sick or healthy

• PCA does not diagnose

• PCA only looks at how test values move together

Panel 3: PCA finds patterns

PCA notices:

• Blood sugar & HbA1c rise together

• Cholesterol & Triglycerides rise together

• BP, ECG & Heart rate move together

So PCA draws three big arrows on the report:

➡️ Arrow 1: Sugar Control
⬆️ Arrow 2: Lipid Health
↗️ Arrow 3: Cardiac Stress

These arrows are the principal components.

Panel 4: Simplified health summary

Instead of 8 test values, the report now shows:

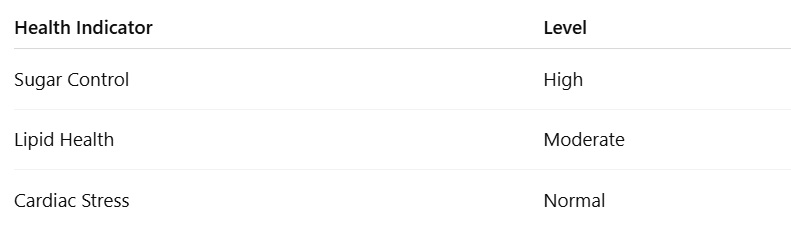
The doctor smiles 😄:

"Now I understand the patient instantly!"

Almost all important information is still there — just cleaner and clearer.

🧠 What PCA did (in simple terms)

• Combined related medical tests

• Reduced complexity

• Found hidden structure

• Made no medical decisions

⚠️ Very important note

PCA does NOT replace a doctor.

It:

• ❌ does not diagnose

• ❌ does not predict disease

• ✅ only summarizes data patterns

One-line takeaway 🎯

PCA turns many medical test numbers into a few overall health indicators without knowing the diagnosis.